変分量子計算を用いたオプションの価格決定

📅 March 24, 2020

•

⏱️13 min read

0

Photo by Sean Pollock on Unsplash

SSRNで論文をみつけて読んでみたが，思ったより闇深いのでメモとして残しておく．

元論文: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3499134

やってることとしては

  • オプションの価格が従う偏微分方程式を，変分量子計算でシミュレーションする．

だけ．シンプルな応用問題である．

実際にこれを用いることで計算が速くなる保証はない． しかし，量子ビット数に対して指数的に大きな空間を扱うことができる．そのため，うまい変分量子回路を構成すれば，古典では空間計算量の都合上扱うことができなかった，大規模な偏微分方程式を解くことができる．これによって，従来より高精度な価格決定が可能になるかもしれない．

また，結構な数のゲートを使うことになるので，現状の実機で動かすのはなかなかに難しいと考えられる．

論文ではヨーロピアンオプションとアジアンオプションについて計算しているが，本稿ではヨーロピアンオプションについてのみ計算する．

ちなみにアメリカンオプションはこのアルゴリズムでは計算できない．偏微分方程式として定式化すると，非線形な項がでてくるが，ベースとなっている変分量子アルゴリズムが線形な偏微分方程式しか解けないからである．(非線形方程式への拡張もあるhttps://journals.aps.org/pra/abstract/10.1103/PhysRevA.101.010301．しかし，これを用いてもアメリカンオプションで出てくるmax⁡\max関数を扱う事はできない．)

そして，この論文，

The results show that a shallow quantum circuit is able to represent European and Asian Call option prices accurately,

と言っているが，shallow circuitで実装する方法は述べられていないし，ansatz以外の部分について具体的な量子回路が提示されていないという問題があることに注意されたい．

まずはオプションの価格が従う偏微分方程式を紹介する．

BSモデル

Black-Scholesモデルでは原資産の変動が幾何ブラウン運動で与えられる．

dSt=rStdt+σdWtdS_t = rS_tdt+\sigma dW_t

ここで，rrは無リスクの金利で，σ>0\sigma>0がボラティリティ，WtW_tが標準ブラウン運動である．

ヨーロピアンコールオプション

ヨーロピアンオプションでは，オプションの行使価格がKKのとき，満期TTにおいて払い戻し関数がf(ST)=max⁡(ST−K,0)f(S_T)=\max(S_T-K,0)となる． このとき，時刻t∈[0,T)t\in [0,T)，原資産価格s>0s>0におけるオプションの価格V(t,St)V(t,S_t)が従う偏微分方程式は

rV(t,St)=∂V(t,St)∂t+σ2St22∂2V(t,St)∂St2+rSt∂V(t,St)∂StrV(t,S_t) = \frac{\partial V(t,S_t)}{\partial t}+\frac{\sigma^2S_t^2}{2}\frac{\partial^2 V(t,S_t)}{\partial S_t^2}+rS_t\frac{\partial V(t,S_t)}{\partial S_t}

となる(Hullなどを参照)．ここで，終端(満期)での条件はV(T,ST)=f(ST)V(T,S_T)=f(S_T)である．これは満期でのヨーロピアンオプションの価値はペイオフと等しいことを表している．

この方程式を，終端条件から時間に関して後ろ向きに解いていく．t=0t=0におけるV(0,S0)V(0, S_0)(つまり，現在時点で原資産価格がS0S_0の点におけるオプションの価値)がヨーロピアンオプションの価格になる．

実際には，ヨーロピアンオプションの場合であれば解析解が求められる．しかし，今回は数値計算で解を得ることを考える．

そういえば，このBS方程式は拡散方程式に変換できることが知られている． St=exS_t=e^x，τ=σ2(T−t)\tau=\sigma^2(T-t)と変数変換すると，

∂u(τ,x)∂τ=12∂2u(τ,x)∂2x\frac{\partial u(\tau, x)}{\partial\tau} = \frac{1}{2}\frac{\partial^2 u(\tau, x)}{\partial^2 x}

となり，熱伝導方程式の形になる．

この形にしておくと，後で変分量子計算するときに扱いやすい．

さて，ここで量子力学っぽく

∣ψ(τ,x)>≔u(τ,x),H^=12∂2∂2x\left| \psi(\tau, x) \right> \coloneqq u(\tau, x),\hat{H} = \frac{1}{2}\frac{\partial^2}{\partial^2 x}

とおいてやると

∂∣ψ(τ,x)>∂τ=H^∣ψ(τ,x)>\frac{\partial \left| \psi(\tau, x) \right>}{\partial\tau} = \hat{H}\left| \psi(\tau, x) \right>

となる．

Variational Quantum Simulation (VQS)

VQSは時間発展方程式を変分量子計算で扱うアルゴリズムである．もちろん，扱える時間発展には条件があるが，Hermiteで無いものも扱えるなど応用範囲が広い．

変分量子計算でよくあるように，VQSではansatzを用いて∣ψ(τ,x)>\left| \psi(\tau, x) \right>を近似する．つまり

∣ψ(τ,x)>≅∣v(θ(t))>\left| \psi(\tau, x) \right> \cong \left| v(\bm{\theta}(t)) \right>

となるようなansatzを導入する．

上記の偏微分方程式を満たすように，このansatzのパラメータの時間発展をうまく調整するのがVQSである．

以下のような変分問題を考える．

δ∥∂∣v(θ(t))>∂τ−H^∣v(θ(t))>∥=0\delta\left\|\frac{\partial \left| v(\bm{\theta}(t)) \right>}{\partial\tau} - \hat{H}\left| v(\bm{\theta}(t)) \right>\right\| = 0

そうすると，パラメータの時間発展が得られる．

∑jMjkθ˙j=Vk\sum_j M_{jk}\dot{\theta}_j = V_k

ここで，Mjk,VkM_{jk}, V_{k}は

Mjk=ℜ(∂<v(θ(t))∣∂θj∂∣v(θ(t))>∂θk)Vk=ℜ(∂<v(θ(t))∣∂θkH^∣v(θ(t))>)\begin{aligned} M_{jk} &= \Re\left(\frac{\partial \left< v(\bm{\theta}(t)) \right|}{\partial \theta_j}\frac{\partial \left| v(\bm{\theta}(t)) \right>}{\partial \theta_k}\right) \\ V_k &= \Re\left(\frac{\partial \left< v(\bm{\theta}(t)) \right|}{\partial \theta_k}\hat{H}\left| v(\bm{\theta}(t)) \right>\right) \end{aligned}

である．

これらは，H^\hat{H}が複素数λi\lambda_i，ユニタリ行列{hj}\{h_j\}によってH^=∑jλihj\hat{H}=\sum_j \lambda_i h_jと展開できるとき下図のような量子回路から計算することができる[https://arxiv.org/abs/1812.08778]．

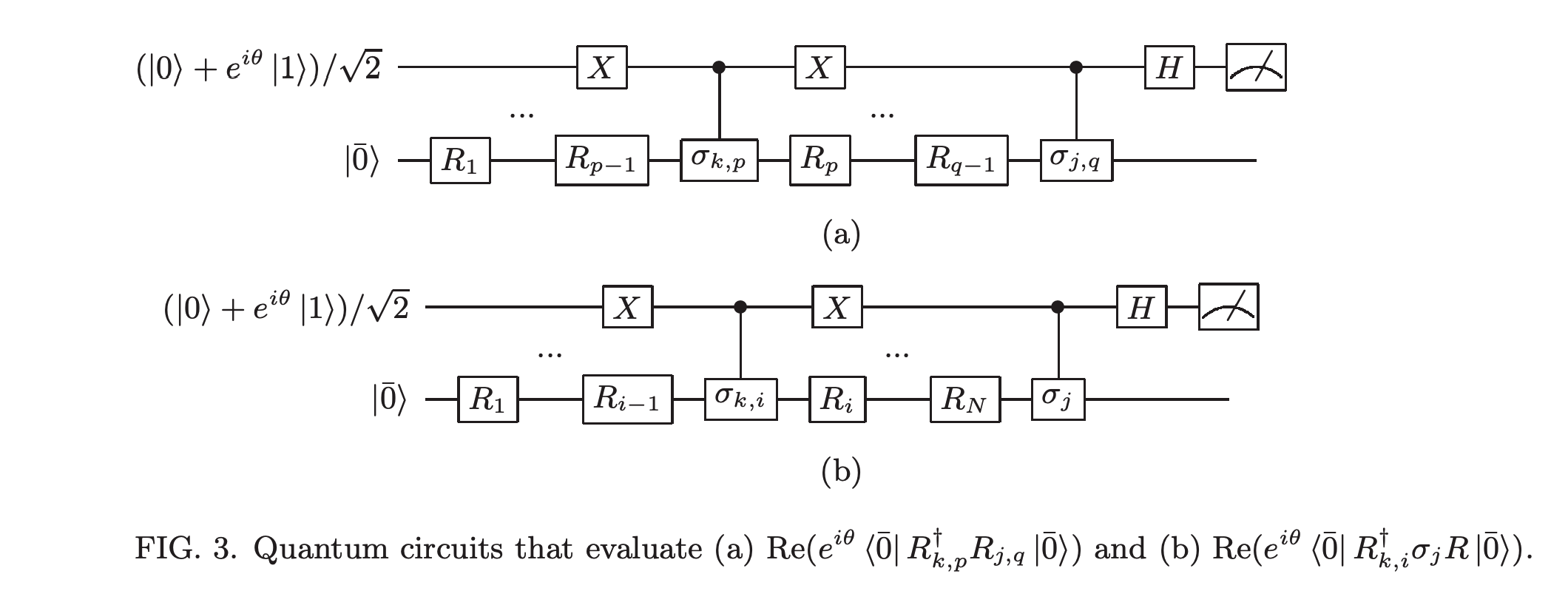
M and V

Mjk,VkM_{jk},V_kを求めたら，パラメータの時間発展を通常の(古典のRunge-Kutta等の)数値計算法を用いて計算してやればよい．

さて，残るは∑jλihj\sum_j \lambda_i h_jの具体的な形と，終端条件，ansatzの用意である．

元論文は∑jλihj\sum_j \lambda_i h_jと終端条件の2つについて不十分である．先にこれらについて説明する．その後，ansatzを紹介する．

∑jλihj\sum_j \lambda_i h_jの準備

量子計算機は有限次元の空間しか扱えないので，H^=12∂2∂2x\hat{H}=\frac{1}{2}\frac{\partial^2}{\partial^2 x}を離散化する必要がある．

これは，

∂2f∂2x≅f(x+Δx)+f(x−Δx)−2f(x)(Δx)2\frac{\partial^2f}{\partial^2 x}\cong\frac{f(x+\Delta x)+f(x-\Delta x)-2f(x)}{(\Delta x)^2}

を用いて離散化すればよい．

論文のほうでは

(−b000⋯00012(Δx)2−1(Δx)212(Δx)20⋯000012(Δx)2−1(Δx)212(Δx)2⋯000⋮⋮⋮⋮⋱⋮⋮⋮0000⋯12(Δx)2−1(Δx)212(Δx)20000⋯00−b)\begin{pmatrix} -b & 0 & 0 & 0 & \cdots & 0 & 0 & 0 \\ \frac{1}{2(\Delta x)^2} & \frac{-1}{(\Delta x)^2} & \frac{1}{2(\Delta x)^2} & 0 & \cdots & 0 & 0 & 0\\ 0 & \frac{1}{2(\Delta x)^2} & \frac{-1}{(\Delta x)^2} & \frac{1}{2(\Delta x)^2} & \cdots & 0 & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \frac{1}{2(\Delta x)^2} & \frac{-1}{(\Delta x)^2} & \frac{1}{2(\Delta x)^2} \\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & -b \end{pmatrix}

となっている．しかし，これをどう量子回路で実装するかについては述べられていない．

ユニタリ行列hj{h_j}の線形結合∑jλjhj\sum_j \lambda_j h_jとして表すには一般に量子ビット数に対して指数個の和が必要になる．これには指数関数的に大きな回数量子回路の測定が必要となるため，量子計算による高速化は得られないと考えられる．

終端条件の用意

時間発展のinitial value problemを解くので，initial valueが必要である．今回の問題設定では時間方向に関して逆向きに解くので，実際には終端条件であるが，これを∣v(θ(0))>\left| v(\bm{\theta}(0))\right>とする．

元論文では

θ(0)=arg min⁡θ∥∣v(θ)>−∣ψ(0)>∥\bm{\theta}(0) = \argmin_{\bm{\theta}}\|\left| v(\bm{\theta})\right>-\left| \psi(0) \right>\|

から，θ(0)\bm{\theta}(0)を用意している．これは非自明な過程であるが，具体的に実行するための量子回路については述べられていない．

ansatz

ansatz

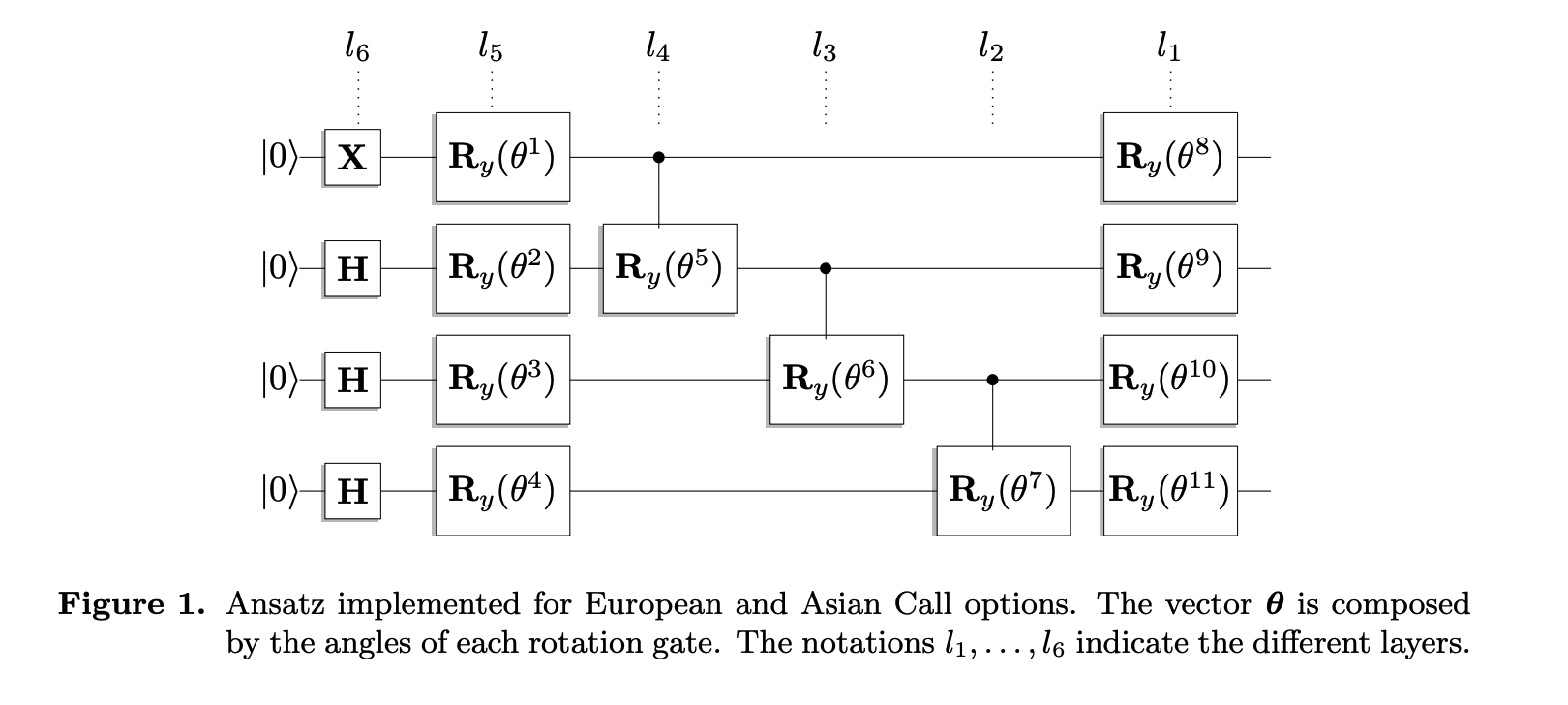
振幅は常に実数であるので，X,HX,Hやエンタングルさせるゲート(図中ではc−Ry\mathrm{c-R_y}ゲート)とRyR_yゲートを用いている．

結果

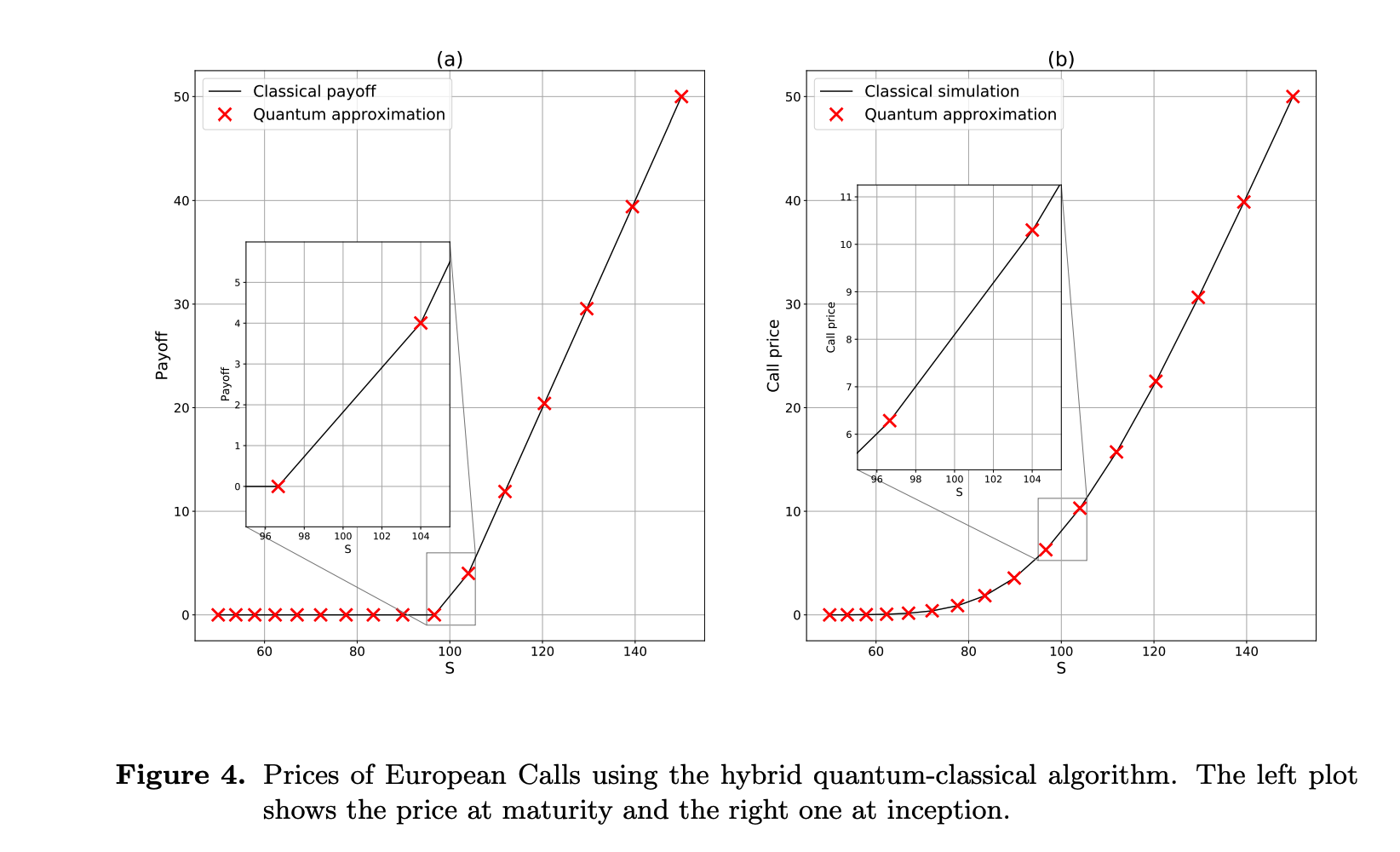
result

4量子ビットでパラメータを25個用いている．結果としては

The hybrid quantum-classical algorithm is able to reconstruct the price function with great accuracy.

と言っているがパラメータが多いので当然である．

色々つっこみどころがあるが，

  1. H^\hat{H}を多項式個のユニタリ行列の線形和として準備する
  2. 初期状態(終端条件)を用意する．
  3. ansatzのパラメータを減らす．

このあたりをクリアして，その上で精度良くオプション価格を計算できれば良いアルゴリズムになるだろう．

0
Next Post →